理论问题环节

为什么我们需要卷积神经网络？

因为全连接神经网络的参数量过大，容易导致模型过拟合

输入必须是3 * 256 * 256吗

不一定，这是一种非常经典且常用的输入尺寸但它并非 CNN 的强制要求，这个尺寸主要来源于早期的经典预训练模型，如AlexNet、VGG、ResNet 等经典预训练模型它们在训练时默认采用了 224×224 的图像分辨率，而 3 代表 RGB 彩色图像的 3 个通道（通道数 × 高度 × 宽度，即 C×H×W）。

每次卷积特征图的尺寸都变小了，如何保持尺度不变呢？

零填充

更大的卷积核和更多的卷积核层数意味着什么？

更大的卷积核意味着更大的感受野，

更多的卷积核层数，就像给模型升级成 “多级侦探”，能从表面细节挖到深层本质，处理更复杂的任务；但层数太多会出现 **“信号断联”的问题（梯度消失 / 爆炸）

梯度消失：指令要经过很多层侦探（层数多），每传一层就被削弱一点，传到最前面的新手侦探时，指令已经弱到听不见了（梯度趋近于 0），新手侦探没法纠正自己的错误，模型学不会。
梯度爆炸：反过来，指令每传一层就被放大一点，传到前面时已经变成 “噪音”（梯度过大），新手侦探收到混乱的指令，越改越错，模型训练崩溃。

卷积核和特征图是什么？

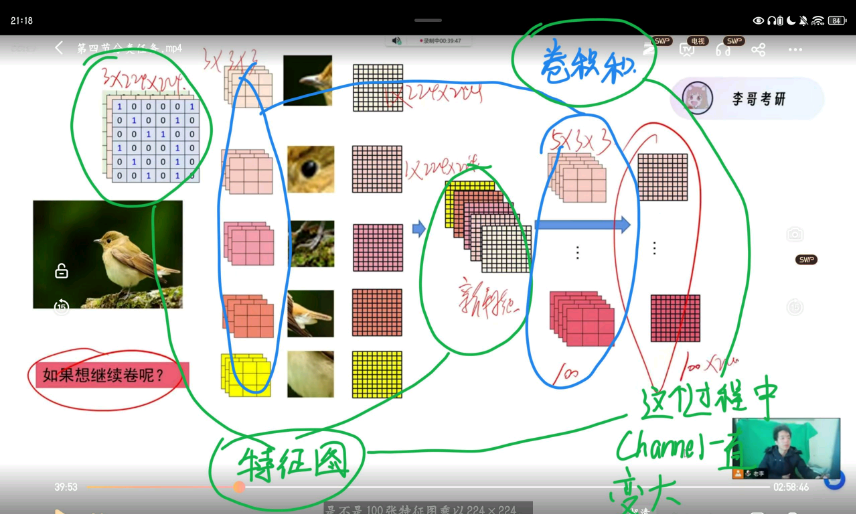
特征图和卷积核的深度有什么关系？

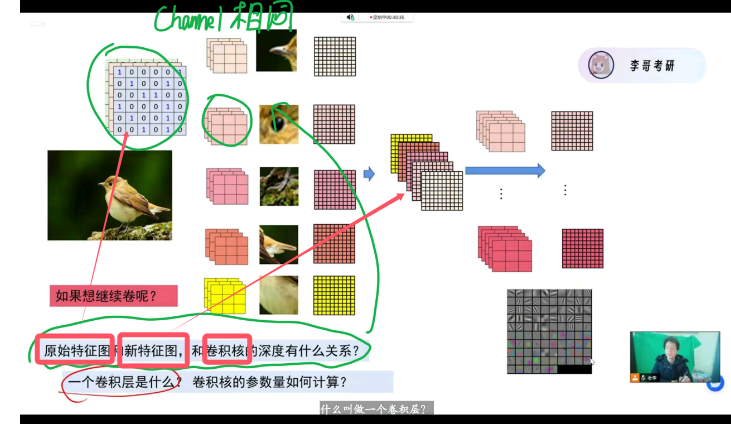
一个卷积层是什么？卷积核的参数量如何计算？

整个模型唯一能控制的量就是卷积层，也可以理解为Conv2d的前三个参数，【输入特征图数量（厚度）】* 【输出特征图数量（厚度）】*【卷积核大小】**2

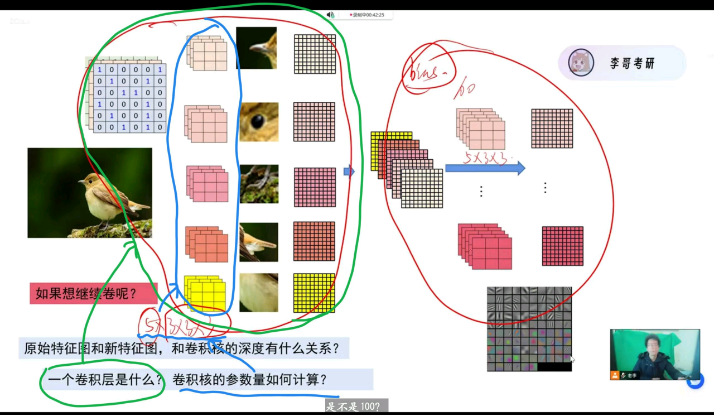
padding如何填充？4 * 4经过一次零填充变成什么样子？

6 * 6

但padding之后特征图大小一直保持不变，仍然需要大量参数怎么办？怎么样才能降低参数量

池化可以把长、宽对半砍

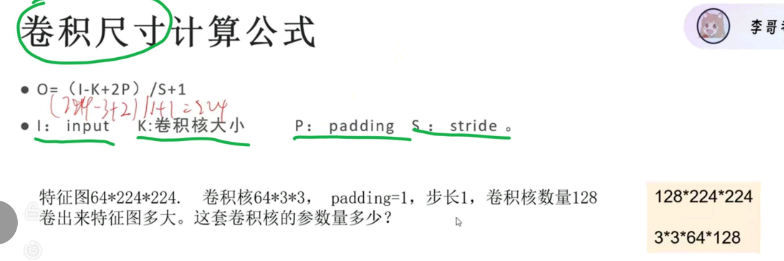
卷积尺寸计算

$$
[
H_{out} = \left\lfloor \frac{H_{in} + 2 \times \text{padding} - \text{kernel_size}}{\text{stride}} \right\rfloor + 1
]
$$

减少特征图尺寸的方法

池化和增加步长都可以减少特征图尺寸**（注意不是减少卷积核的参数）**，但池化一般比增加步长更常用。

所以如何改变图片的参数大小呢？

不要忘记初心，我们一开始是为了分出一个类别

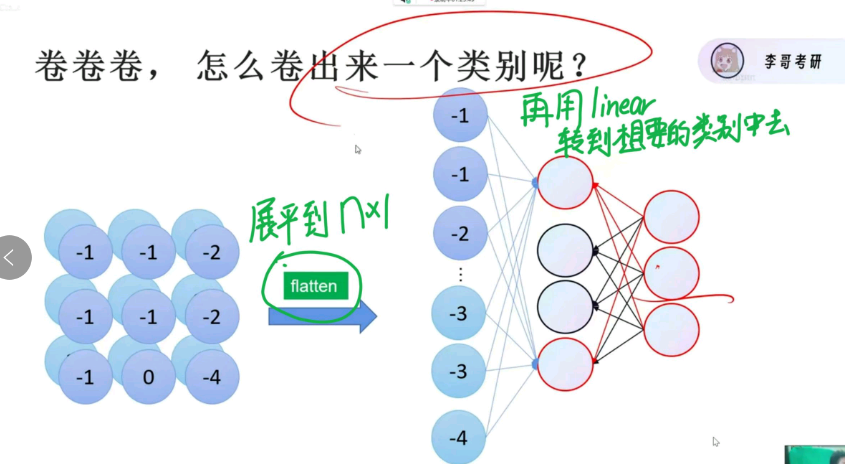
loss如何衡量？

使用softmax，把计算出来的、差距不大的数值，转变成最终的、差距很大的概率

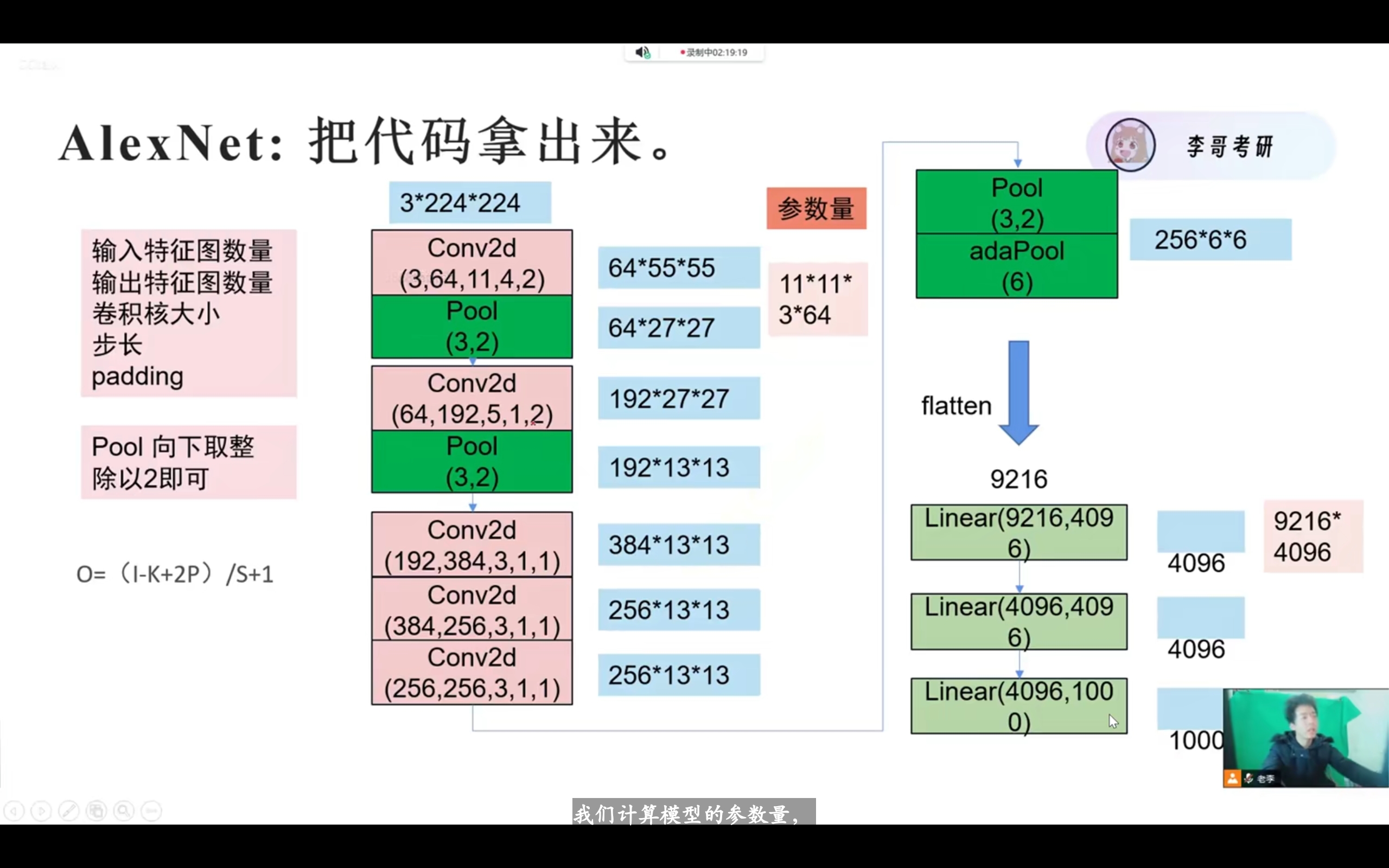
经典神经网络AlexNet做了什么改进？

relu、dropout、池化、归一化

Conv2d参数

（输入特征图数量（厚度），输出特征图数量（厚度），卷积核大小，步长，padding）

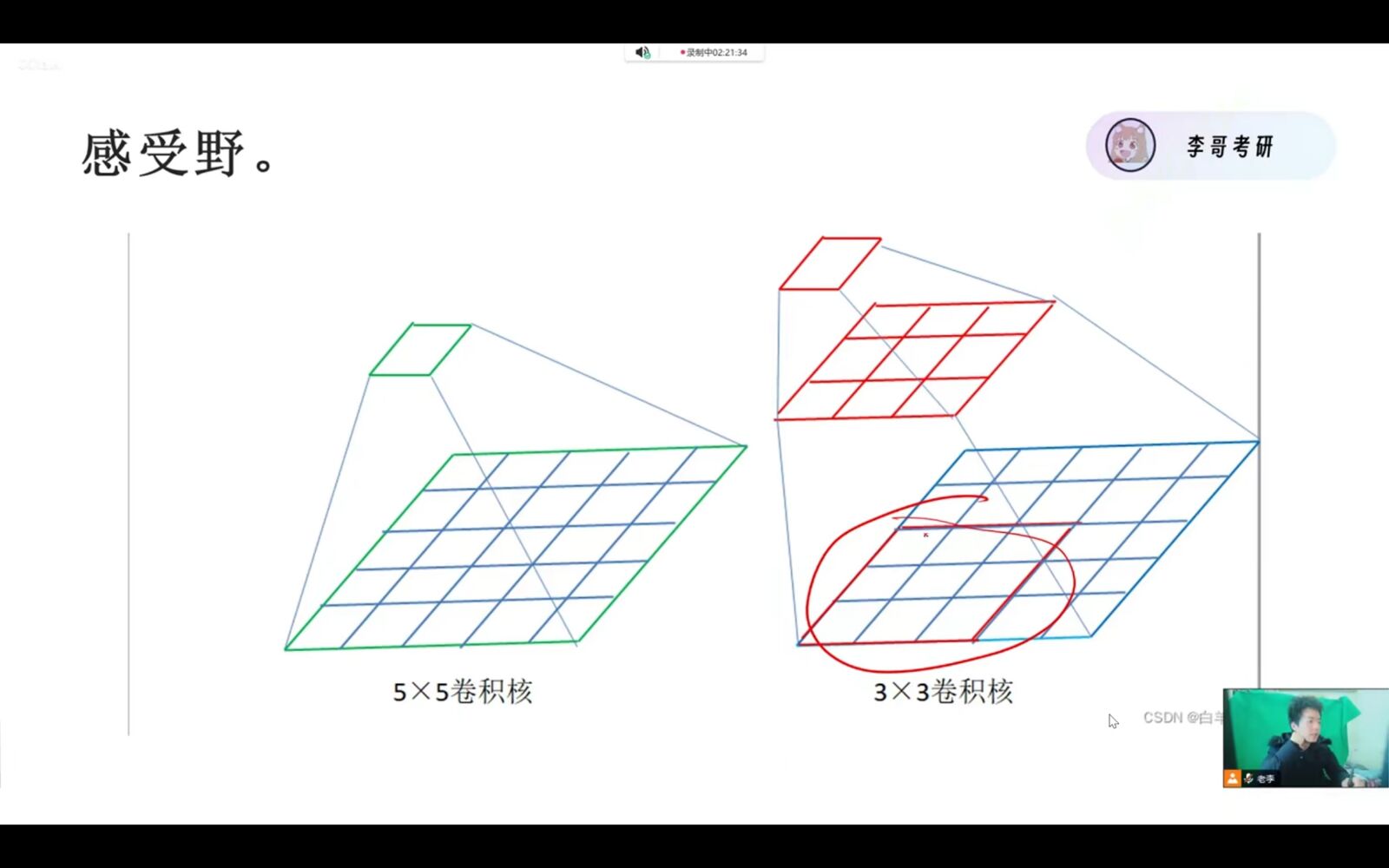
VGG做了什么改善？

使用小的卷积核替代了大的卷积核，缩小了感受野，减少了参数量。如可以用两个三乘三的卷积核替代五乘五的卷积核，这样参数的数量由25个减少至18个

363a840e55309a0e9c8f77d0ee2afc7a

resNet做了什么改善？

第一，使用残差连接，解决梯度消失和梯度爆炸

梯度消失和梯度爆炸是要解决的问题，梯度爆炸可以通过relu或sigmoid解决，但梯度消失不容易解决。

由于梯度回传本身就是一个求导的过程。

resNet令out = f(x) + x，这样求到之后可以保证大于一，这样就缓解了梯度消失的问题。

同时，这也解释了为什么relu比sigmoid更不容易消失，因为relu梯度始终为一，而sigmoid当x过大时导数过小。

73295a6630df84d3a8ead08549a7f711

但这也会遇到一个问题：f(x)和x的尺寸不一样咋办？

答案是resNet的另一个作用：1* 1卷积

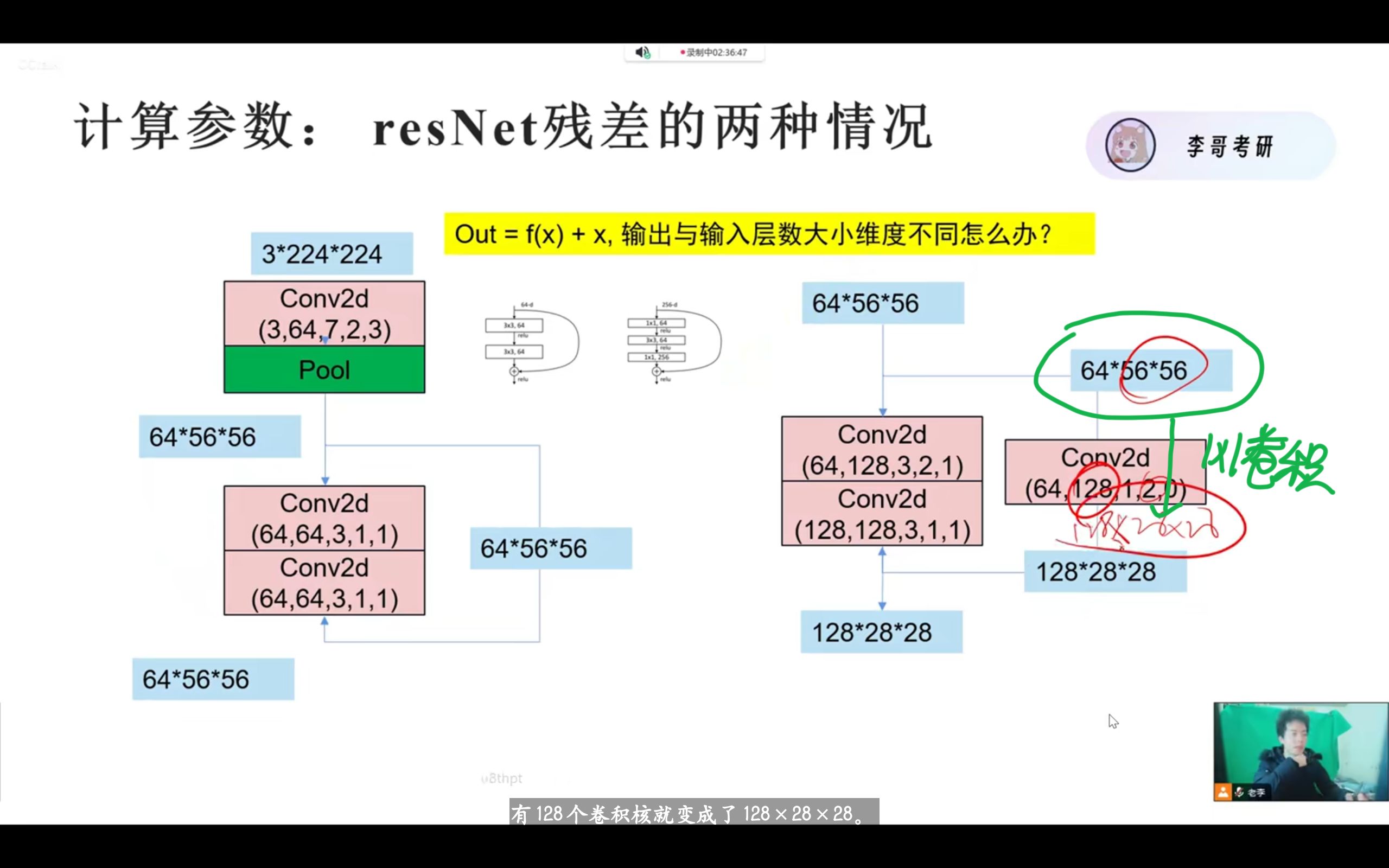
fe79e3bf61909d05b1b3c4ece4e5182e

第二，使用1*1卷积，减少参数量，给数据降维

1*1卷积的核心不在于1 * 1，而在于输入输出的厚度变化。

对应 Conv2d(256,64,1,1,0)：输入通道 256，输出通道 64，通过 1×1 卷积将通道数从 256 压缩到 64，实现通道降维。

通俗类比：把 256 张 “特征图片”（每个通道对应一张特征图），通过加权融合，浓缩成 64 张更核心的 “特征图片”，既保留关键信息，又减少后续计算的 “素材量”。

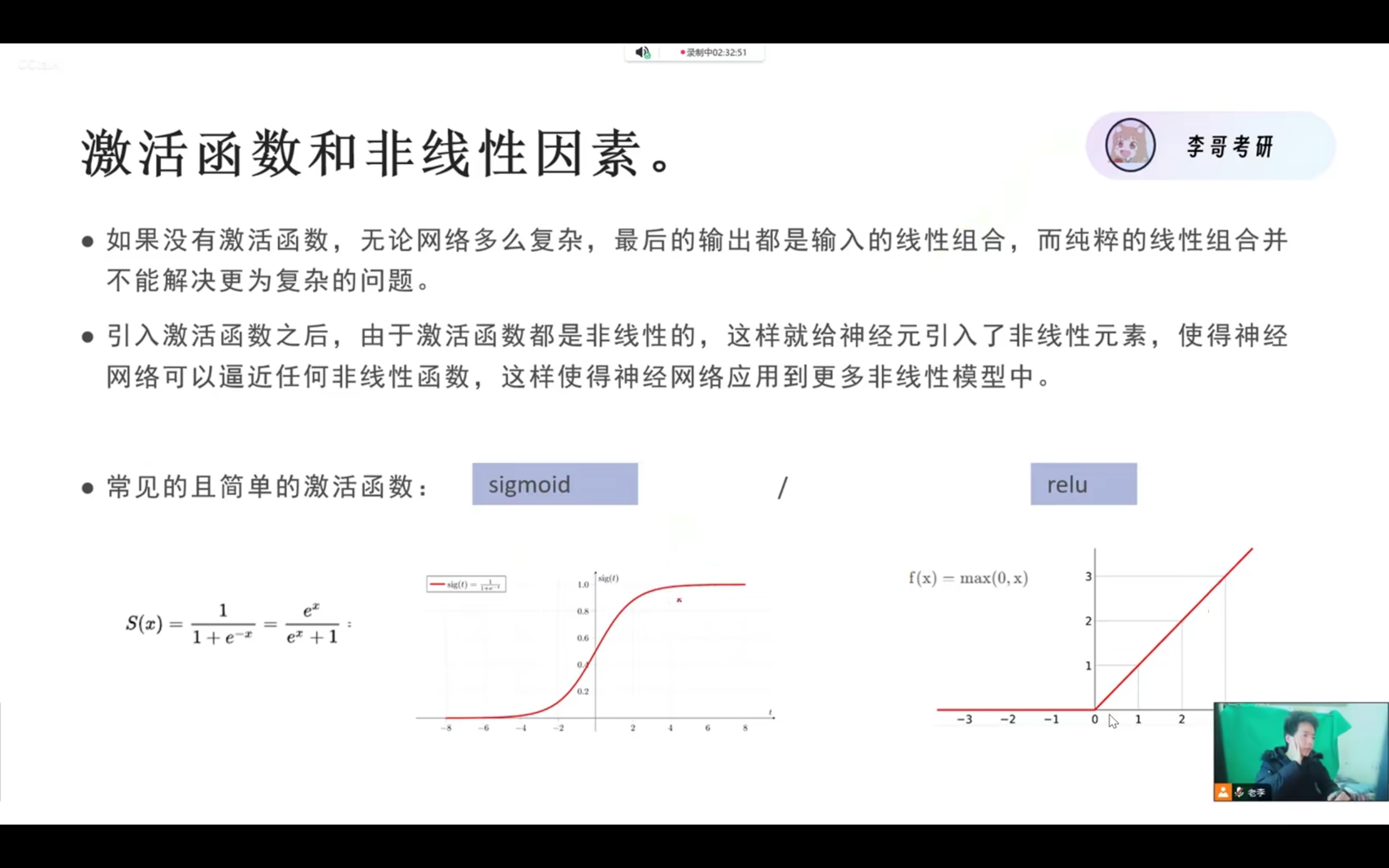
为什么需要引入激活函数

引入激活函数的根本目的是 为神经网络注入 “非线性能力”，让模型能够学习和拟合现实世界中的复杂非线性关系（如图像分类、语言翻译等）；如果没有激活函数，无论神经网络有多少层，本质上还是一个线性模型，无法解决复杂任务。

线性操作的叠加，结果还是线性

神经网络中的卷积层（nn.Conv2d）、全连接层（nn.Linear），本质上都是线性变换（数学上可表示为 y = Wx + b，其中 W 是权重、b 是偏置）。

比如：一个两层的线性网络，第一层输出 y1 = W1x + b1，第二层输出 y2 = W2y1 + b2，代入后可得 y2 = W2(W1x + b1) + b2 = (W2W1)x + (W2b1 + b2)，这依然是一个线性表达式（只是权重和偏置变了）。

也就是说：无论你叠加多少层线性层，最终的输出和输入之间，依然是简单的线性关系，多层网络和单层线性模型没有本质区别，相当于 “白搭了多层结构”。

代码实践

构造并运行模型

54716fe6edffd8060f94f0eeb191886e

class myModel(nn.Module):
    def __init__(self, num_cls):
        super(myModel,self).__init__()
        self.conv1 = nn.Conv2d(3,64,11,4,2)
        self.pool1 = nn.MaxPool2d(3,2)

        self.conv2 = nn.Conv2d(64, 192, 5, 1, 2)
        self.pool2 = nn.MaxPool2d(3, 2)

        self.conv3 = nn.Conv2d(192, 384, 3, 1, 1)
        self.conv4 = nn.Conv2d(384, 256, 3, 1, 1)
        self.conv5 = nn.Conv2d(256, 256, 3, 1, 1)

        self.pool3 = nn.MaxPool2d(3,2)
        self.pool4 = nn.AdaptiveAvgPool2d(6)

        self.fc1 = nn.Linear(9216,4096)
        self.fc2 = nn.Linear(4096,4096)
        self.fc3 = nn.Linear(9216,num_cls)

def forward(self,x):
    x = self.conv1(x)
    x = self.pool1(x)
    x = self.conv2(x)
    x = self.pool2(x)
    x = self.conv3(x)
    x = self.conv4(x)
    x = self.conv5(x)
    x = self.pool3(x)
    x = self.pool4(x)

    x = x.view(x.size()[0], -1)  # 拉直。 batch
    x = self.fc1(x)
    x = self.fc2(x)
    x = self.fc3(x)
    return x

x = x.view(x.size()[0], -1)的作用？

保持x的第一维不变，将其他维展开至一维。即保留批次大小不变，自动将高维张量展平为二维张量，为卷积层和全连接层搭建数据传输的桥梁，是 CNN 模型中不可或缺的扁平化操作。